LeetCode精选TOP面试题50.Pow(x, n)

2022-03-17
阅读量 | 字数：645字 | 预计阅读时长：3分钟

题目描述

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn ）。

example
input  : x = 2.00000, n = 10
output : 1024.00000
input  : x = 2.10000, n = 3
output : 9.26100
input  : x = 2.00000, n = -2
output : 0.25000
note   : 2^-2 = 1/2^2 = 1/4 = 0.25

解题思路

公式：

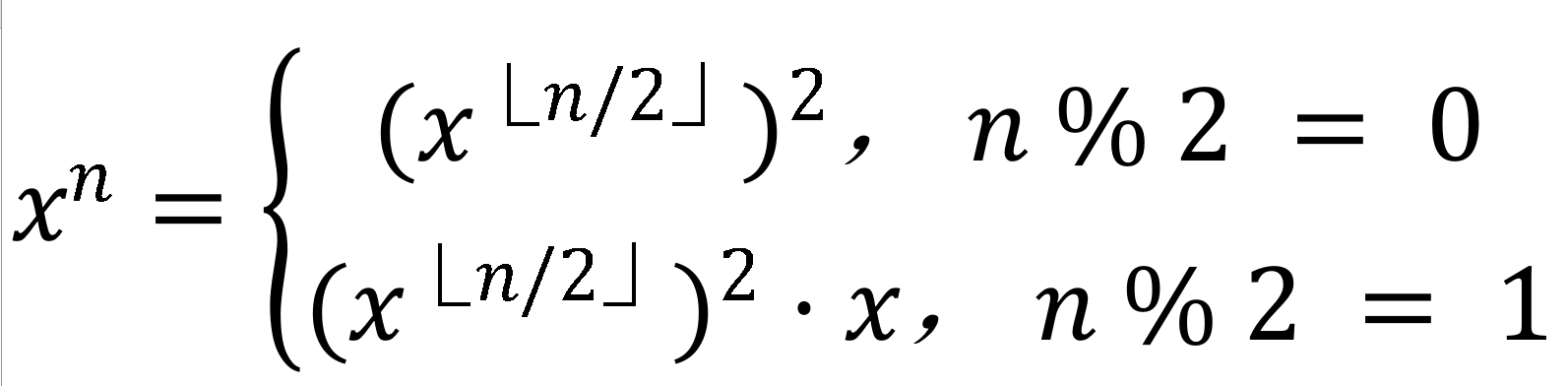
思路1 递归

参数：初始值 x，指数 m
退出边界：m = 0，返回1，任何数的0次幂都是1
递归主体：y = loop(x, m / 2)，此处y等价于公式中的 x^⌊n/2⌋次幂，⌊n/2⌋代表下取整，如⌊7/2⌋ = 3
返回值：当 m 是奇数，返回 y * y * x；当 m 是偶数，返回 y * y
时间复杂度：O(log n)
空间复杂度：O(log n)

思路2 迭代

当 n 为奇数时，二分后会多出一项 x （当前的x值，不是初始的x值）。
可通过循环 x = x^2 操作，每次把幂从 n 降至 ⌊n/2⌋ ，直至将幂降为 0；
设 res = 1，则初始状态 x^n = x^n · res ；
在循环二分时，每当 n 为奇数时，将多出的一项 x 乘入 res ，则最终可化至 xn = x0 · res = res；
最后返回 res 即可。
算法主要流程：
- 当n < 0时，把问题转化到 |n| >= 0 的范围内，即执行 n = -n，x = 1 / x操作
- 初始化res = 1
- 循环，当n = 0时结束：
  - 当 n % 2 = 1时，将 当前的x 乘入 res
  - 执行 x = x^2，令当前 x 扩大至其平方值
  - 执行 ⌊n/2⌋，降幂（降至n = 0时循环结束）
时间复杂度：O(log n)
空间复杂度：O(1)
参考自题解

思路3 暴力

for循环逐个乘
无法通过测试，超出时间限制
时间复杂度：O(n)
空间复杂度：O(1)

代码（Java）

思路1代码

public class Solution1 {
    public double myPow(double x, int n) {
        // 为了防止n由负数转为正数时的溢出，先用long接收n
        long m = n;
        return m > 0 ? loop(x, m) : 1.0 / loop(x, -m);
    }

    private double loop(double x, long m){
        if (m == 0) {
            return 1.0;
        }
        double y = loop(x, m /2);
        return m % 2 == 0 ? y * y : y * y * x;
    }
}

思路2代码

public class Solution2 {
    public double myPow(double x, int n) {
        if (x == 1) {
            return 1;
        }
        long m = n;
        if (m < 0) {
            x = 1.0 / x;
            m = -m;
        }
        double result = 1.0;
        while (m > 0) {
            if (m % 2 == 1) {
                result = result * x;
            }
            x = x * x;
            m /= 2;
        }
        return result;
    }
}

思路3代码

public class Solution3 {
    public double myPow(double x, int n) {
        if (x == 1) {
            return 1;
        }
        long m = n;
        if (m < 0) {
            x = 1.0 / x;
            m = -m;
        }
        double result = 1.0;
        for(long i = 0; i < m; i ++){
            result = result * x;
        }
        return result;
    }
}

本文作者： whtli
本文链接： https://hexo.whtli.cn/archives/42e9890.html
版权声明： 遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。