原文：Kalisch M, Buehlmann P. Estimating high-dimensional directed acyclic graphs with the PC-algorithm. J Mach Learn Res 2007;8:613–36.
原文网页版
Web of science
Abstract
本文研究了PC算法用于估计具有相应高斯分布的高维有向无环图（DAG）的骨架和等价类。 对于有许多节点（变量）的稀疏问题，PC算法在计算上是可行的，而且往往非常快，它具有吸引人的特性，可以自动实现高计算效率，作为真实底层DAG的稀疏程度的函数。本文证明了该算法在高维稀疏DAGs中的一致性，并允许节点数量随样本大小n快速增长，对于任何0 < a <∞快如$O(n^a)$。稀疏性假设是相当最小的，只要求DAG中的邻域的阶数低于样本容量n。文章还演示了模拟数据的PC算法。
1. Introduction
图模型是一种用来分析和可视化随机变量之间的条件独立性关系流行的概率工具。模型的主要构建模块是节点（代表随机变量）和边（编码了顶点的条件独立性关系）。随机变量之间的条件独立性结构可以使用马尔可夫性质来探索。
当前的研究兴趣是有向无环图（DAG），它包含有向边而不是无向边，这在一定程度上限制了条件独立性关系。这些图可以应用马尔可夫性质来解释。当忽略DAG的方向，可以得到一个DAG的骨架。通常来说，它和条件独立性图（CIG）是不同的，见2.1节（因此，有向图的估计方法不能简单地借鉴无向的CIG的估计方法）。2.1节中可以看到，骨架可以很容易地解释，从而对数据的依赖结构产生有趣的见解。
由于DAG空间的巨大规模，从数据中估计DAG是困难的，在计算上也是不可行的：可能的DAG的数量在节点数量上是超指数的。然而，针对中小规模节点数量，有一些十分成功的的 搜索-评分方法。例如，搜索空间可能像MWST那样被限制为树结构，或者采用贪婪的搜索方式。如GES (Greedy Equivalent Search, see Chickering, 2002a) 方法所述，贪婪的DAG搜索可以通过利用概率等价关系来优化，且搜索空间可以从单个DAG缩小到等价类。尽管这种方法在中小规模的节点数量情况下似乎很有前途，但它受限于一个事实，即等价类的空间在节点数量增长时也是超指数增长的 (Gillispie and Perlman, 2001)。
一个有趣的替代贪婪或者结构限制的方法是Spirtes等人在2000年提出的PC算法。它从一个完备的无向图开始，基于条件独立性决策递归地删除边。这会生成一个无向图，然后它会被部分地定向，并进一步扩展以表示底层的DAG。PC算法在最坏的情况下是以运行时间是运行的，但是如果真实的底层DAG是稀疏的（这通常是一个合理的假设），运行时间将会缩减为多项式时间。
在过去，提出了一些有趣的混合方法，最近，Tsamardinos等人(2006)提出了一种计算上非常有竞争力的算法。本文还参考了他们的论文，在广泛的算法之间进行了相当详尽的数值比较研究。
本文主要研究了在高维环境下DAGs的等价类和骨架的估计（对应于多元高斯分布），即节点数p可能远远大于样本数n。本文证明，当样本大小n→∞时，即使允许维数 $p = p_n = O(n^a) (0 ≤ a ＜∞)$作为n的函数快速增长，PC算法也能一致地估计出底层稀疏DAG地等价类和骨架。
如第4.5节所示，本文对PC算法的实现速度惊人地快，它允许估计一个稀疏的DAG，即使p很大。对于p远大于n的高维设定，底层DAG的稀疏性对于统计一致性和计算可行性是至关重要的。本文的分析似乎是第一次为高维DAG建立了一个可证明的正确算法（在渐进意义上），该算法在计算上是可行的。
关于包括PC算法在内的一类方法的一致性问题已经被Sprites等人和Robins等人在因果推断的文章讨论过。他们证明，只假设忠实性（第二节中有说明），统一一致性无法实现，但点状一致性可以实现。在本文中，本文用两种方式对其进行了扩展：本文提供了一套假设，使PC算法具有统一的一致性。更重要的是，本文证明即使是当节点数和邻居数增加，并且最小的非零协方差作为样本量的函数而减小，这个一致性也能始终保持。Zhang和Spirtes（2003）也提出了比忠实性条件更严格的假设，使均匀一致成为可能。Zuk等人（2006）对学习正确的贝叶斯网络结构需要多少样本的更普遍的讨论。
寻找DAG的等价类的问题与特征选择问题有很大的重合：如果找到了等价类，则可以很容易地读取任意变量(节点)的马尔可夫毯。给定一个节点集合V，假设M是节点X的马尔科夫毯，那么在给定M的条件下，X与V\M是条件独立的。因此，M包含且只包含所有的X的相关特征。例如，见Goldenberg和Moore(2004)关于处理非常高的维度的方法，或Ng(1998)关于处理泛化误差的界限的相当普遍的方法。
2. Finding the Equivalence Class of a DAG
在本节中，首先说明主要的概念。然后，给出关于PC算法的详尽描述。
2.1 Definitions and Preliminaries
图 G=(V, E) 由一组顶点V={1，…，p} 和一组边 E⊆V×V 组成，即边集是不同节点的有序对的子集。在本文的设定中，节点集对应于随机变量X∈R^p^ 的分量。如果 (i, j)∈E 且(j, i)/∈E ，则边 (i, j)∈E 被叫做有向边，用符号i→j 表示。如果 (i, j)∈E 且 (j, i)∈E ，则该边被叫做无向边用符号 i-j 表示。一个有向无环图（DAG）是一个所有边都是有向边且不包含环的图。
如果存在有向边 i→j ，则节点i是节点 j 的父节点。节点j的父节点的集合用 pa(j) 表示。节点 j 在图 G 中的邻居集合用 adj(G, j) 表示，它表示所有直接和 j 通过边（有向或者无向）连接的节点。 adj(G, j) 中的节点也被称为j的邻居或者与 j 相邻。
如果 $R^p$上 的概率分布 P 中的条件独立性可以从图 G 的d-separation中被推断出来，反之亦然，则 P 忠诚于图 G 。更精确的说：考虑一个随机向量 X~P 。 P 的忠诚性意味着：对于任意的 i,j∈V 且 i≠j ，则对于任意的 s⊆V 有
$X^{(i)}$ and $X^{(j)}$ are conditionally independent given ${X^{(r)}; r ∈ s}$
⇔ node i and node j are d-separated by the set s.
d-separation的概念可以由道德图定义；详见Lauritzen的描述 (1996,Prop. 3.25)。在此指出，忠实性是排除某些类别的概率分布的。Spirtes等人（2000，第3.5.2章）给出了一个非忠实分布的例子。另一方面，多元正态族（本文将限制在此）的非忠诚分布在与DAG G相关的分布空间中形成一个Lebesgue 空集，见Meek(1995a)。
DAG G 的骨架是用无向边代替 G 中的有向边得到的无向图。DAG G 中的 v-structure 是一个有序的三元节点组 (i, j, k) 使得G包含有向边 i→j 和 k→j ，并且 i 和 k 在G中不相邻。
众所周知，对于一个由DAG G 生成的概率分布 P ，存在一个完整的具有对应分布 P 的等价类DAGs (见 Chickering, 2002a, Section 2.2 )。即使有无限多的观察结果，本文也无法区分一个等价类中的不同DAG。利用Verma和Pearl(1990)的一个成果，可以更精确的描述等价类的特征。当且仅当两个DAG有相同的骨架和相同的v-structure时，他们是等价的。
常用的DAG等价类的可视化工具是完备的部分有向无环图（CPDAG）。一个部分有向无环图（PDAG）是一个部分边有向且部分边无向的图。PDAG之间或PDAG和DAG之间的等价性可以通过检查骨架和V形结构来决定，就像DAG一样。一个PDAG是完备的，如果：(1)在属于DAG等价类的每个DAG中也存在相应的有向边，且(2)对于每条无向边 i−j ，在等价类中存在一个带i→j的DAG和一个带 i←j 的DAG。
CPDAG编码了相应的等价类中包含的所有独立性信息。Chickering（2002）证明，当且仅当两个CPDAG表示的是同一个等价类时，它们是等价的，即，它们表示的是同一个等价类。
尽管主要目标是确定CPDAG，骨架本身已经包含了有趣的信息。尤其是，如果概率分布P忠诚于一个DAG G，
there is an edge between nodes i and j in the skeleton of DAG G
⇔ for all $s ⊆ V \ {i, j}, X^{(i)}$ and $X^{(j)}$ are conditionally dependent given ${X^{(r)}; r∈s}$,(1)
(Spirtes et al., 2000, Th. 3.4). 这表明如果概率分布P对于一个DAG G来说是忠诚的，则DAG G的骨架是对应于P的条件独立性图（CIG）的真子集（或子集）。原因是CIG中的一条边只需要在给定集合V \ {i, j} 的情况下有条件依赖性。更重要的是，骨架张的每条边都表示某种强依赖，其不能通过其他变量来解释。本文认为，这个性质对探索性分析很有意义。
在接下来的细节内容中将看到，估计CPDAG主要由两部分组成（这自然地组成了本文地分析结构）：（1）骨架的估计（2）部分边的定向。所有统计推断都在第一部分完成，第二部分只是对第一部分的结果应用确定性的规则。因此本文将更多的注意力放在第一部分上，如果第一部分操作正确，那么第二部分将永远不会失败。但是，如果在第一部分中出现错误，第二部分将对它更加敏感，因为它更详细地依赖于(1)的推断结果。当处理高维设定时（p大，n小），CPDAG比骨架的恢复更加困难。此外，对于CPDAG的解释更多地依赖于图的全局正确性。而对于骨架的解释只依赖于局部区域，因此更可靠。
本文的结论是，如果真实的底层概率机制是由DAG生成的，那么找到CPDAG是主要目标。骨架本身通常已经提供了有趣的见解，在高维设定中，当找到一个有用的CPDAG的近似似乎没有希望时，使用无向骨架作为CPDAG的替代目标可能是有趣的。
综上所述，本文接下来将描述两个主要步骤。首先，文章讨论PC算法生成骨架图的部分。之后文章将通过讨论寻找CPDAG的扩展来完成该算法。在讨论PC算法理论性质的时，文章将使用相同的格式。
2.2 The PC-algorithm for Finding the Skeleton
寻找骨架的一种朴素的策略是检查给定所有子集s⊆V \ {i, j}(见公式1)的”条件独立性”，也就是说，如Verma和j . pearl(1991)首次提出的，在多元正态分布情况下的所有”偏相关”。当p大于样本量时，这在计算上是不可行的，在统计上也是不恰当的。PC算法使用了一个更好的办法，它可以利用图的稀疏性。更准确地说，文章应用PC算法的一部分来识别DAG的无向边。
2.2.1 POPULATION VERSION FOR THE SKELETON
在PC算法地population版本中，文章假设对所有必要地条件独立性都有充分地了解。这里指的PC算法是别人所说的PC算法的第一部分；另一部分在第2.3节的算法2中描述。
PC算法的第一部分在Algorithm1中给出。算法1中 l 的最大值可表示为
$m_{reach}$ = maximal reached value of l. (2)
$m_{reach}$的值取决于底层分布。
从Spirtes等人（2000）中的定理5.1中，可以很容易地推导出该算法会生成正确的骨架。文章总结如下。
Proposition 1 考虑一个DAG G并假设分布P忠诚于G。标记最大邻居数为 $q=max_{1≤j≤p}|adj(G, j)|$。然后，$PC_{pop}$ 算法构建DAG的真实骨架。此外，$m_{reach}∈{\lbrace q-1, q\rbrace}$
（原文附录A中给出了证明。）
2.2.2 SAMPLE VERSION FOR THE SKELETON
对于有限的样本，需要估计条件独立性。本文将自身限制在高斯情况下，其中所有节点都对应于具有多元正态分布的随机变量。此外，本文假设忠诚性模型，这意味着条件独立关系对应于d-separation (因此可以从图中读出)，反之亦然；见第2.1节。
在高斯情况下，可以从偏相关性中推断出条件的独立性。
Proposition 2 假设随机变量X的分布P是多元正态分布。对于$i ≠ j\in {1,…, p}, k⊆{\lbrace 1,…, p\rbrace}\setminus {\lbrace i, j\rbrace}$，使用符号$\rho_{i,j\mid k}$来表示$X^{(i)}$和$X^{(j)}$在给定 $\lbrace X^{(r)};r\in k \rbrace$时的偏相关性。那么，当且仅当$X^{(i)}$和$X^{(j)}$在给定$\lbrace X^{(r)};r\in k \rbrace $条件独立时$\rho_{i,j\mid k}$的值为0。
证明：该主张是多变量正态分布的一个基本属性，见Lauritzen(1996, Prop. 5.2.)。
因此可以估计偏相关性，以获得条件独立性的估计。样本偏相关性$\hatρ$可以通过回归，部分协方差矩阵的反演，或者使用以下恒等式来递归计算：对于h∈k，
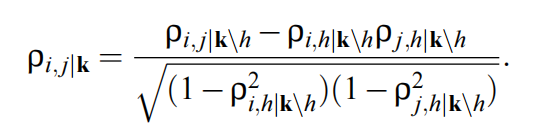
本文使用的是递归方法（上式，即第三种方法）。为了检验偏相关系数是否为0，本文使用Fisher’s z-transform对偏相关系数进行转换。
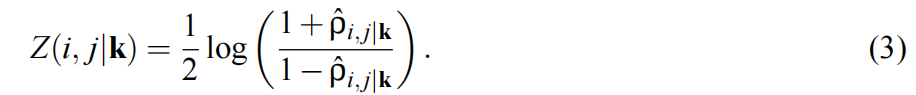
当使用显著性水平α时，经典决策理论生成了以下规则。$H_0$和$H_A$。当$sqrt(n−|k|−3|)Z(i,j|k)|>Φ^{−1}(1−α/2)$时，接受$H_A:\rho_{i,j|k}≠0$；拒绝$H_0:\rho_{i,j|k}=0$；其中Φ(·)代表N(0, 1)的累积分布函数。
用 $sqrt(n−|k|−3|)Z(i,j|k)| ≤ Φ^{−1}(1−α/2)$替换 $PC_{pop}$算法 中的第11行：“if i and j are conditionally independent given k then”。该算法产生一个依赖于数据的值$\hat{m}_{reach}$，它是公式(2)的样本版本。
$PC_{pop}$ 算法的唯一调优参数是α，这是检验偏相关性的显著性水平。
正如将在第3节中看到的，即使p远大于n，但当DAG是稀疏的，该算法也是渐进一致的。
2.3 Extending the Skeleton to the Equivalence Class
在寻找算法1中的骨架时，记录了使边缘在由S表示的变量中消失的分离集。这对于寻找骨架本身来说是不必要的，但对于将骨架扩展到等价类来说是必不可少的。在算法2中，描述了Pearl(2000, p.50f)的工作，将骨架扩展到属于底层DAG的等价类的CPDAG。
算法2的输出是一个CPDAG，这是由Meek（1995b）首次证明的。
3. Consistency for High-Dimensional Data
由第二节可以看到，首先处理寻找骨架的问题。接下来，将结果扩展到寻找CPDAG。
3.1 Finding the Skeleton
本文将证明第2.2.2节中的PC算法对于DAG的骨架是渐进一致的，即使p远大于n，而DAG是稀疏的。本文假设数据是i.i.d.（独立同分布）的向量$X_1, …, X_n，X_i∈R^p$ 来自有对应分布P的DAG G。为了观察高维行为，本文将使维数作为样本大小的函数增长：因此，$p=p_n$，且$DAG~G=G_n$，分布$P = P_n$。假设如下：
- （A1）对于任意的n，分布P
n是多元正态分布且忠诚于DAG $G_n$。 - （A2）维数$p_n=O(n^a)，0≤a＜∞$
- （A3）$DAG~G_n$中的最大邻居数表示为 $q_n=max_{1≤j≤p_n}|adj(G,j)|$，与$q_n=O(n^{(1−b)}), 0<b≤1$。
- （A4）对于集合$k⊆{\lbrace1，…，p_n}\rbrace \setminus {\lbrace i, j\rbrace}$，给定{X^(r)^; r∈k}时，$X^{(i)}$和$X^{(j)}$之间的偏相关用 $ρ_{n;i,j|k}$ 表示。它们的绝对值有上界和下界：
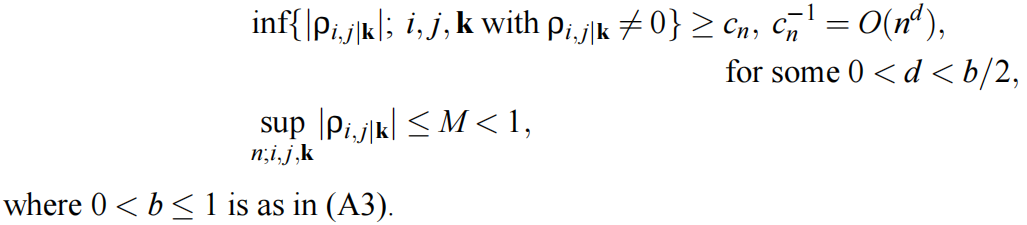)（A1）是图模型中常用的假设，尽管它确实限制了可能的概率分布类型（见2.1节的第三段）；（A2）允许维度作为样本量的函数的任意多项式增长，即高维度；（A3）是稀疏假设；（A4)是正则性条件。定理1如下图：
3.2 Extending the Skeleton to the Equivalence Class
如前所述，所有的推理都是在寻找骨架时完成的。如果这部分完美地完成，也就是说，如果在测试条件独立性时没有错误（假设骨架被正确估计是不够的），第二部分将永远不会失败（见Meek，1995b）。因此，很容易得到定理2：
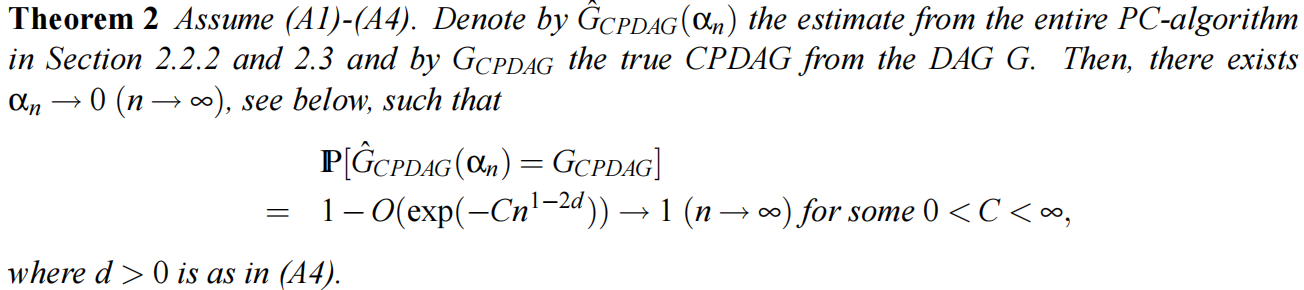
4. Numerical Examples
本文分析了PC算法使用各种模拟数据集来寻找骨架和CPDAG。利用R语言的pcalg包得到了数值结果。关于对不同算法的广泛的数值比较研究，文章参考了Tsamardinos等人的文章（2006）。
4.1 Simulating Data
4.2 Choice of Significance Level
文章中通过多组对比实验，认为α=0.005或α=0.01时的拟合效果最好。
4.3 Performance for Different Parameter Settings
为了保持概述在一个可管理的大小，文章将后续实验的显著性水平限制为α = 0.01。
4.4 Properties in High-Dimensional Setting
从某种意义上说，DAG的真实边的百分比的稀疏性是下降的，而在另一种意义上，邻域大小的稀疏性是随着n的增加而增加的。
4.5 Computational Complexity
PC 算法的计算复杂度难以精确计算，但最坏情况是以作为维数p的函数的公式(4)为界的。
5. R-Package pcalg
R语言包pcalg可用于从数据中估计DAG的底层骨架或等价类。若要使用此软件包，就需要安装统计软件R。R和R包都可以在http://www.r-project.org免费获得。对于低维问题（但不是对于成百成千上万的p），还有许多pc算法的其他实现也值得一提：
• Hugin at http://www.hugin.com .
• Murphy’s Bayes Network toolbox at http://bnt.sourceforge.net .
• Tetrad IV at http://www.phil.cmu.edu/projects/tetrad .
接下来将展示一个如何使用R包pcalg生成随机DAG，抽取样本并从数据中推断原始DAG的骨架和等价类。结果骨架和CPDAG中的边的线宽可以被调整，以对应于估计得到的依赖关系的可靠性。(线宽与✓(n−|k|−3)Z(i, j, k)的最小值成正比。因此，粗线是可靠的)。
示例代码（原文和新版本R包）
原文版本 Old example in this paper(the new version of R-package)
library(pcalg)
## define parameters
# number of random variables
p <- 10
# number of samples
n <- 10000
# sparsness of the graph
s <- 0.4
## generate random data
set.seed(42)
# generate a random DAG
g <- randomDAG(p, s)
# generate random samples
d <- rmvDAG(n, g)
## Note : pcAlgo is DEPRECATED in the new version of pcalg package, and the new method 'pc', 'skeleton' is recommended.
# estimate of the skeleton
gSkel <- pcAlgo(d, alpha=0.05)
gCPDAG <- udag2cpdag(gSkel)
# The CPDAG can also be estimated directly using
gCPDAG <- pcAlgo(d, alpha=0.05, directed=TRUE)
## plot the graph
plot(g)
plot(gSkel, zvalue.lwd=TRUE)
plot(gCPDAG, zvalue.lwd=TRUE)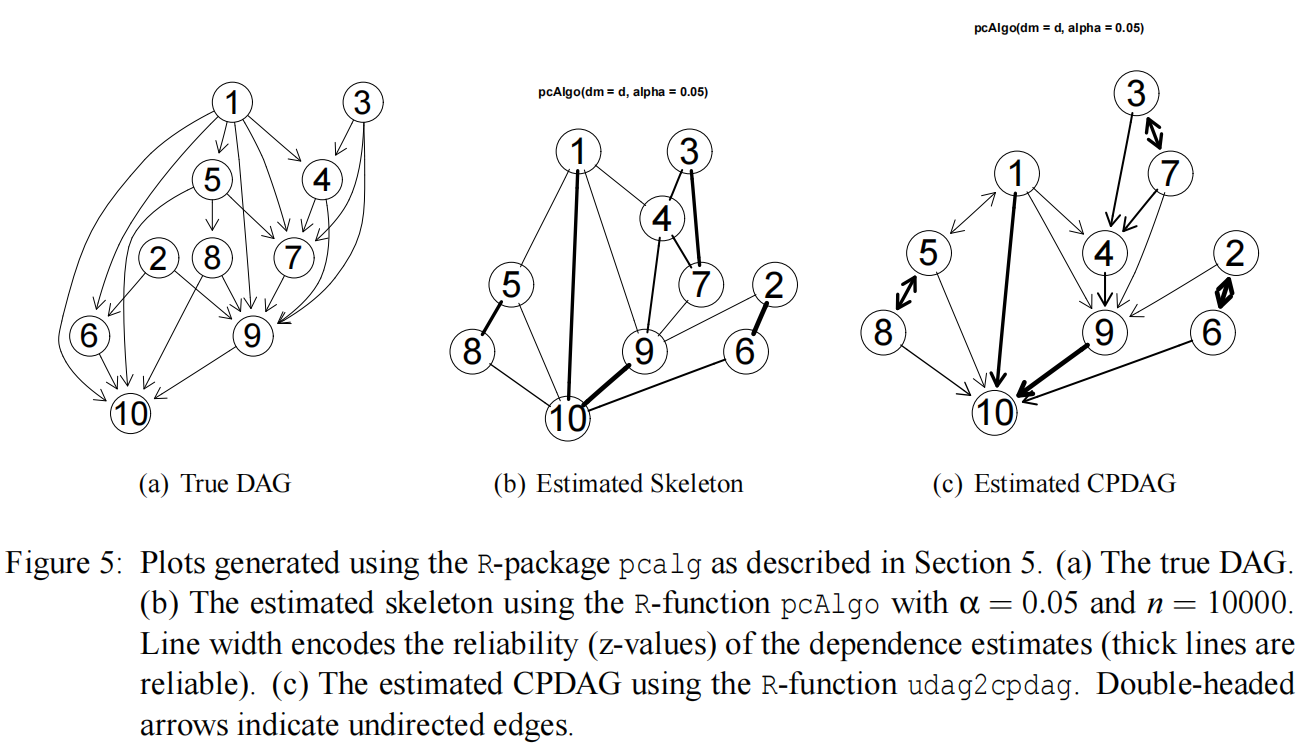
新的R包版本 New example in the new version of R-package
## Using Gaussian Data
library(pcalg)
library(Rgraphviz)
library(graph)
library(BiocGenerics)
library(grid)
# Load predefined data
data(gmG)
n <- nrow(gmG8$x)
# labels aka node names
V <- colnames(gmG8$x)
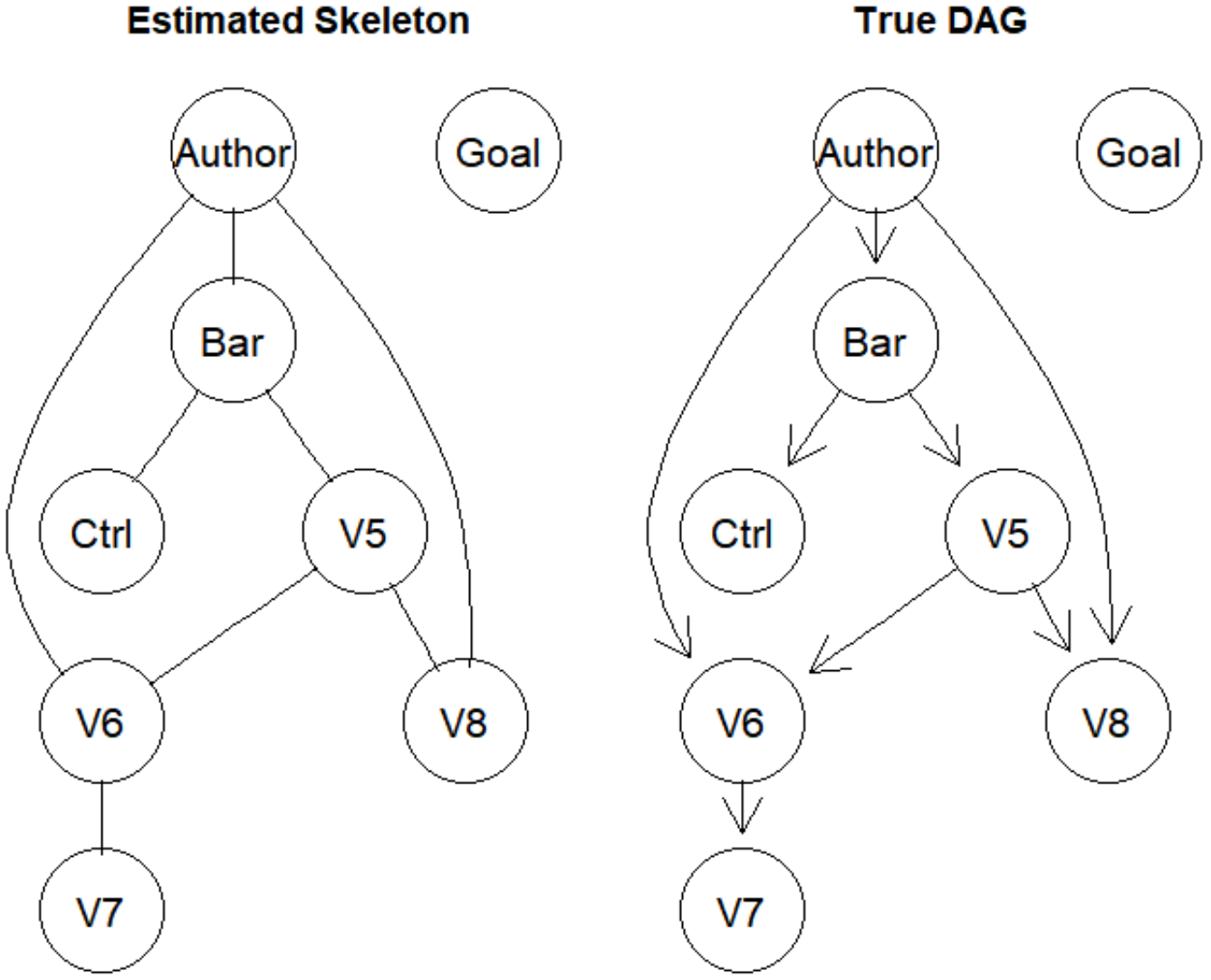
# estimate skeleton
skel.fit <- skeleton(suffStat = list(C = cor(gmG8$x), n = n), indepTest = gaussCItest, alpha = 0.01, labels = V, verbose = TRUE)
if (require(Rgraphviz)) {
## show estimated Skeleton
par(mfrow=c(1,2))
plot(skel.fit, main = "Estimated Skeleton")
plot(gmG8$g, main = "True DAG")
}
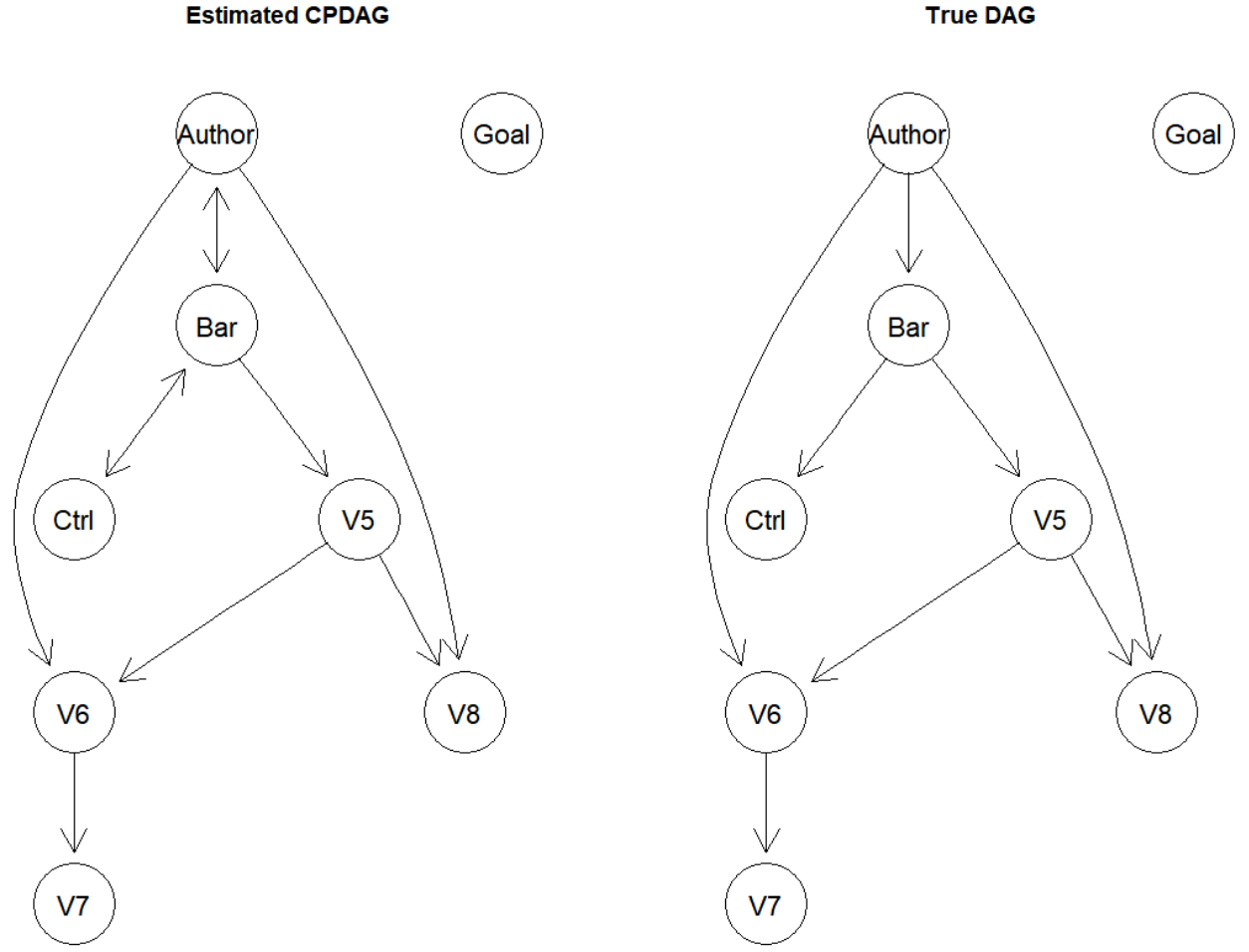
# estimate CPDAG
pc.fit <- pc(suffStat = list(C = cor(gmG8$x), n = n), indepTest = gaussCItest, alpha = 0.01, labels = V, verbose = TRUE)
if (require(Rgraphviz)) {
## show estimated CPDAG
par(mfrow=c(1,2))
plot(pc.fit, main = "Estimated CPDAG")
plot(gmG8$g, main = "True DAG")
} 
6. Conclusions
本文表明，对于DAG（由CPDAG表示）及其骨架的等价类，PC算法是渐进一致的，具有相应的高维稀疏高斯分布。此外，PC算法对于这种高维、稀疏的问题在计算上是可行的。把这两个事实放在一起，PC算法被确立为一种方法（到目前（文章发表于2007年）为止是唯一的一种），它在计算上是可行的，并且在统一一致性的意义上是可以证明正确的，适用于高维DAGs。稀疏性，即真正底层DAG的邻域的最大大小，对于统计一致性和计算可行性至关重要，其复杂度最多是作为维数函数的多项式。
文章强调，DAG的骨架经常提供有趣的见解，在高维环境下，使用无向的骨架作为更简单但更现实的目标而不是整个CPDAG是非常明智的。
本文链接： https://hexo.whtli.cn/archives/3abfd6b2.html
版权声明： 遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。